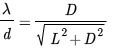A bucket filled with water to a height h has a blocked hole on the bottom. The measurements of both the height h and the height of the hole from the bottom of the bucket is measured. Taking th difference between these two measurements gives the height of the hole to the surface of water. Measuring as accurately as possible, the height h is 13.6 cm and the height from the bottom is 2.5 cm both with an uncertainty of +- .05 cm giving the height from the hole to the surface of the water as 11.1 cm +- .10 cm. The diameter of the hole is measured again as accurately as possible giving a value of .55 cm +- .05 cm. The area of that hole can then be calculated by taking half the diameter, squaring it, then multiplying by pi.

The volume emptied chosen was to 400 mL of water which was then measured by a beaker. 6 trials were done in measuring the time needed to empty the 400 mL of water and they came out to 15.9, 13.32, 12.45, 12.65, 12.61, and 13.39 seconds. Due to human errors and reaction time the uncertainty of each of these time intervals was +- 0.15 seconds. The average time of these six trials was calculated as 13.39 +- 2.02 seconds.
Using the volume emptied 400 mL, area of drain hole 2.38 * 10^-5 m/s, acceleration due to gravity 9.8 m/s/s, and height of water 11.1 cm, the theoretical time taken given by:

The theoretical time was calculated to be 11.41 seconds. The difference between actual and theoretical values were all between 1.20 and 4.49 seconds, but the 4.49 seconds deviates greatly from the rest and is an outlier. Calculating the percent errors on the times between actual and theoretical values came to be 39%, 16%, 9.1%, 10.8%, 10.5%, and 15.6%. This was given by the universal formula of error percent:

Even using the values of uncertainty, the experimental values did not agree with the theoretical values entirely. All the time difference errors were near 1 to 4 seconds uncertainty did not calculate to be that great. To correct this problem a greater value of uncertainty should be estimated. Fluid experiments seem to have larger uncertainty than some branches of physics because the exact volume measured is more difficult to catch precisely. Other main uncertainties come from reaction time of starting the stopwatch and stopping it since this requires two people. The biggest form of uncertainty comes from the inaccurate volume measurement since water is flowing fairly quickly and it is less obvious to tell what the volume is precisely. The beaker itself has an uncertainty when filling up because of how precise the beaker is constructed. Many beakers, graduated cylinders, and other glassware contain an uncertainty and it is printed on the glassware. For example 500 mL +-.5 mL.



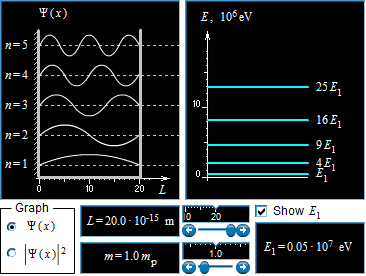
 This is the energy of the ground state this can also be written as E = h^2/8mL this is the equation derived and given for an atom in ground state for a particle in a box. As the length of the box in this denoted as L increases then the value of the energy is decreased. It is inversely proportional to the ground state energy of an atom.
This is the energy of the ground state this can also be written as E = h^2/8mL this is the equation derived and given for an atom in ground state for a particle in a box. As the length of the box in this denoted as L increases then the value of the energy is decreased. It is inversely proportional to the ground state energy of an atom.