Experiment 10: Lenses

The objective of this experiment is to determine a relationship between the object distance d0, the image distance di, and the image height hi. This can be accomplished by increasing the focal length by an integer value each trial. The first step that must be done is to determine the focal length of the magnifying glass that is being used. This can be determined by taking the convex lense outside where the sun is and continue adjusting the length until the focal length can be determined. Measure this using a ruler and the focal length for the lense was 24.5 cm.

As the object distance is changed to half the focal length, the focal point could not be seen because the image was blurry and cannot be focused on. Graphs were to be plotted with the object distance vs the image distance with the object distance on the x values and the image distance on the y values.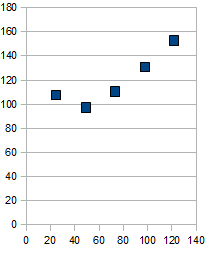

This is not a linear graph but the graph of the inverse is more linear:

Using the computer's best line fit for the equation, the resulting line is y = -.87337x + .03788 which determines a lot about the graph of the inverses. The y intercept of .03788 determines the inverse of the focal length which is simply just 1/y intercept. The slope of the line indicates the relation of the focal point and the object distance. In the form of y = mx + b, the actual equation becomes 1/p = -m(1/q) + 1/f.


Just like any other experiment, there is always a certain amount of uncertainty. Especially with this lab and the lab where the width of a human hair is measured, slight uncertainty results can result in a much larger field of error. The most obvious uncertainty in this experiment comes from the human error. When the focal length was measured outside when using the sun as a source of light, many factors can contribute in giving an inaccurate measurement. However, the trial is done twice to minimize the amount of error given off by measurements. The other factor of uncertainty is basically the same thing, when one measures with the ruler, the measurements will always become off by a small but damaging amount.

Experiment 9: Concave and Convex Mirrors

This experiment contains very few materials since it is more of a conceptual lab. Most of the lab is done by just observations, and then applying those observations with the geometric drawing to determine whethere they agree with each other. The equipment or materials needed for this lab are simple: obviously a convex and concave mirror, a ruler, and an object. There are two main parts for each the convex and concave mirror. The first part consists of writing observations of how the mirrors play a role in the reflection of light waves, and secondly to determine the trigonometric angles to determine the height of the image and the magnification using scaling techniques.

The first part of the two mirrors is a convex mirror, which is a mirror that is rounded outward rather than inward. Any object will suffice such as my hand, and thus using this object in front of the convex mirror, the image appears larger in the middle, but smaller on the outside. The image on the mirror is upright rather than inverted. The image is located closer relative to the position of the mirror and object. As one moves the object closer to the mirror, the new image gets much larger fairly quickly. Likewise, as one moves the object further form the mirror than the previous observations, the new image gets much smaller quickly.

The second part of the convex mirror part is to determine the magnification of an image using simple geometric ways. The drawing above is basically recreated and the magnification is to be determined. The definition of magnification is the height of the image divided by the height of the object. The magnification of this convex mirror is .8cm / 3.3 cm which came out to be about .24x magnification. The observations did agree with the light ray sketch because the magnification is smaller.

For the concave mirrors, things are a little bit different than in the convex mirrors. Concave just means a mirror that is bent inward rather than outward which seems sort of like a cave hence the name. The image appears larger than the object instead of smaller like the convex because of the different ways the light reflects off the surface. The image also appears inverted from far, but upright from close. This must be because the focal point is in front of the mirror, rather than behind. So once the focal point is passed, the image becomes inverted. The image is located farther relative to the position of the mirror and object, whereas in convex it was the opposite.

After the observations of the concave mirror have been made, it is time to start the geometric applications of the light to this mirror. Just like how it was done for the convex mirror, a ruler will be used to show the reflection of the light rays bouncing off the surface of the mirror. The ruler is used to measure the distance of the object, the height of the object, the distance of the image, and the height of the image. In the end, the only two needed variables are the height of the image and the height of the object which are divided by each other to get a magnification of -.26x. This is nearly the same but negative as the magnification of the convex mirror. In a world without uncertainty, these would be exactly opposite values, but however due to human error and the thickness of the lead in a pencil, these will contribute factors of uncertainty. Even though they are minor and may be neglected, these are the only uncertainties that this lab will have.